| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 & 2 (Before Exercise 4.1) | Exercise 4.1 | Example 3 (Before Exercise 4.2) |
| Exercise 4.2 | ||
Chapter 4 Data Handling
Welcome to this comprehensive solutions guide for Chapter 4, "Data Handling," meticulously crafted for the latest Class 8 NCERT mathematics textbook for the academic session 2024-25. This chapter significantly builds upon previous knowledge of data analysis, introducing students to more sophisticated methods for organizing large datasets and employing advanced graphical representations like histograms and pie charts. It also revisits and reinforces the fundamental concepts of probability. Mastering these techniques is crucial for interpreting information critically and making sense of statistical data encountered in various academic and real-world contexts. These solutions provide detailed, step-by-step explanations for all exercises, ensuring clarity and enabling students to develop strong data literacy skills.
When dealing with large amounts of raw data, simple frequency tables become unwieldy. This chapter introduces the powerful technique of organizing data into grouped frequency distribution tables. The solutions provide clear guidance on this process, explaining key concepts such as:
- Class Intervals: Defining ranges (e.g., 10-20, 20-30) to group the data.
- Class Size: The width of each class interval (e.g., the class size for 10-20 is 10).
- Upper and Lower Class Limits: The maximum and minimum values defining each interval.
A key focus is on the visual representation of grouped data using Histograms. The solutions clearly distinguish histograms from bar graphs, emphasizing that histograms are used for continuous grouped data and have no gaps between the bars (representing the continuous nature of the class intervals). Detailed steps for constructing histograms are provided, covering selecting appropriate scales for the axes (x-axis for class intervals, y-axis for frequency), labeling them accurately, and drawing adjacent rectangular bars whose heights correspond to the frequencies of their respective class intervals. Equally important is the interpretation of existing histograms – the solutions demonstrate how to extract information, such as identifying the interval with the highest frequency or comparing frequencies across different intervals.
Another powerful visualization tool explored is the Pie Chart (or Circle Graph), ideal for representing the proportion of different components within a whole dataset. The solutions provide meticulous guidance on constructing pie charts:
- Calculating the fraction or percentage each component represents out of the total.
- Calculating the central angle for each sector (component part) using the formula: $\text{Central Angle} = \left( \frac{\text{Value of the component}}{\text{Total value}} \right) \times 360^\circ$.
- Accurately drawing the circle and using a protractor to draw each sector corresponding to its calculated central angle.
The chapter revisits Probability, focusing on calculating the likelihood of events based on experiments or observed data. The solutions reinforce the fundamental definition: $P(\text{Event}) = \frac{\text{Number of outcomes favourable to the event}}{\text{Total number of possible outcomes}}$ They guide students in systematically listing all possible outcomes for simple experiments (like rolling dice, tossing coins, drawing cards, using spinners), identifying the outcomes that constitute a specific event, and then calculating its probability.
Regarding the rationalized syllabus for 2024-25, Chapter 4, "Data Handling," in the Class 8 NCERT textbook has maintained its focus on grouped frequency distributions, histograms, pie charts, and basic probability. The rationalization process primarily involved streamlining the number and complexity of exercises, potentially removing the construction of frequency polygons or some highly intricate data interpretation questions, ensuring students master the core representation techniques and probability concepts effectively. By engaging with these detailed solutions, students can learn advanced data organization and visualization methods, become proficient in constructing and interpreting histograms and pie charts, and solidify their understanding of fundamental probability calculations.
Example 1 & 2 (Before Exercise 4.1)
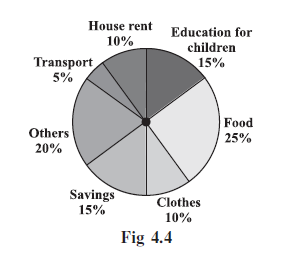
Example 1: Adjoining pie chart (Fig 4.4) gives the expenditure (in percentage) on various items and savings of a family during a month.
(i) On which item, the expenditure was maximum?
(ii) Expenditure on which item is equal to the total savings of the family?
(iii) If the monthly savings of the family is ₹ 3000, what is the monthly expenditure on clothes?
Answer:
Solution:
Given:
A pie chart showing the percentage expenditure on various items and savings of a family.
The percentages shown in the pie chart are:
Food: $25\%$
Education for Children: $15\%$
Savings: $15\%$
House Rent: $10\%$
Clothes: $10\%$
Transport: $5\%$
Others: $20\%$
(i) On which item, the expenditure was maximum?
To find the item with maximum expenditure, we need to look for the item with the highest percentage in the pie chart.
Comparing the percentages for all items of expenditure (excluding Savings):
Food: $25\%$
Others: $20\%$
Education for Children: $15\%$
House Rent: $10\%$
Clothes: $10\%$
Transport: $5\%$
The highest percentage is $25\%$, which corresponds to Food.
Therefore, the expenditure was maximum on Food.
(ii) Expenditure on which item is equal to the total savings of the family?
First, find the percentage for Savings from the pie chart. Savings is $15\%$.
Now, look for an item of expenditure that has the same percentage as Savings.
Checking the percentages of expenditure items:
Food: $25\%$
Education for Children: $15\%$
House Rent: $10\%$
Clothes: $10\%$
Transport: $5\%$
Others: $20\%$
The expenditure on Education for Children is $15\%$, which is equal to the percentage of Savings ($15\%$).
Therefore, the expenditure on Education for Children is equal to the total savings of the family.
(iii) If the monthly savings of the family is ₹ 3000, what is the monthly expenditure on clothes?
From the pie chart, Savings represent $15\%$ of the total monthly income/expenditure.
We are given that the monthly savings is $\textsf{₹}\ 3000$.
So, $15\%$ of the total monthly income/expenditure = $\textsf{₹}\ 3000$.
Let the total monthly income/expenditure be $T$.
$15\% \text{ of } T = \textsf{₹}\ 3000$
$\frac{15}{100} \times T = 3000$
To find $T$, multiply both sides by $\frac{100}{15}$:
$T = 3000 \times \frac{100}{15}$
$T = \frac{300000}{15}$
$T = 20000$
The total monthly income/expenditure is $\textsf{₹}\ 20000$.
Now, we need to find the monthly expenditure on Clothes. From the pie chart, the expenditure on Clothes is $10\%$ of the total monthly income/expenditure.
Expenditure on Clothes = $10\% \text{ of } T$
Expenditure on Clothes = $10\% \text{ of } \textsf{₹}\ 20000$
Expenditure on Clothes = $\frac{10}{100} \times 20000$
Expenditure on Clothes = $10 \times 200$
Expenditure on Clothes = $2000$
The monthly expenditure on clothes is $\textsf{₹}\ 2000$.
Example 2: On a particular day, the sales (in rupees) of different items of a baker’s shop are given below.
| ordinary bread | 320 |
| fruit bread | 80 |
| cakes and pastries | 160 |
| biscuits | 120 |
| other | 40 |
| Total | 720 |
Draw a pie chart for this data.
Answer:
Given:
Sales of different items in a baker's shop.
Ordinary bread: $\textsf{₹}\ 320$
Fruit bread: $\textsf{₹}\ 80$
Cakes and pastries: $\textsf{₹}\ 160$
Biscuits: $\textsf{₹}\ 120$
Other: $\textsf{₹}\ 40$
Total Sales: $\textsf{₹}\ 720$
To Draw:
A pie chart for the given data.
Solution:
To draw a pie chart, we need to find the central angle of the sector for each item. The total of the central angles in a pie chart is $360^\circ$.
The central angle for each component is calculated as:
Central Angle for a component = $\frac{\text{Value of the component}}{\text{Sum of the values}} \times 360^\circ$
Let's calculate the central angle for each item:
Ordinary bread:
Central Angle = $\frac{320}{720} \times 360^\circ = \frac{320}{2} = 160^\circ$
Fruit bread:
Central Angle = $\frac{80}{720} \times 360^\circ = \frac{80}{2} = 40^\circ$
Cakes and pastries:
Central Angle = $\frac{160}{720} \times 360^\circ = \frac{160}{2} = 80^\circ$
Biscuits:
Central Angle = $\frac{120}{720} \times 360^\circ = \frac{120}{2} = 60^\circ$
Other:
Central Angle = $\frac{40}{720} \times 360^\circ = \frac{40}{2} = 20^\circ$
Let's verify the sum of the central angles:
$160^\circ + 40^\circ + 80^\circ + 60^\circ + 20^\circ = 360^\circ$. The sum is correct.
We can summarize the data with calculated central angles in a table:
| Item | Sales ($\textsf{₹}$) | Fraction of Total Sales | Central Angle |
| Ordinary bread | 320 | $\frac{320}{720}$ | $\frac{320}{720} \times 360^\circ = 160^\circ$ |
| Fruit bread | 80 | $\frac{80}{720}$ | $\frac{80}{720} \times 360^\circ = 40^\circ$ |
| Cakes and pastries | 160 | $\frac{160}{720}$ | $\frac{160}{720} \times 360^\circ = 80^\circ$ |
| Biscuits | 120 | $\frac{120}{720}$ | $\frac{120}{720} \times 360^\circ = 60^\circ$ |
| Other | 40 | $\frac{40}{720}$ | $\frac{40}{720} \times 360^\circ = 20^\circ$ |
| Total | 720 | $\frac{720}{720} = 1$ | $160^\circ + 40^\circ + 80^\circ + 60^\circ + 20^\circ = 360^\circ$ |
Now, we can draw the pie chart using these central angles.
Steps to draw the pie chart:
1. Draw a circle with any convenient radius.
2. Draw a radius to start marking the angles.
3. Using a protractor, draw sectors with the calculated central angles ($160^\circ$, $40^\circ$, $80^\circ$, $60^\circ$, $20^\circ$) one by one, starting from the end of the previous sector.
4. Label each sector with the corresponding item name and/or its value/percentage.
5. Give the pie chart a suitable title, such as "Sales of a Baker's Shop".
Exercise 4.1
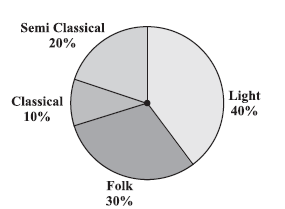
Question 1. A survey was made to find the type of music that a certain group of young people liked in a city. Adjoining pie chart shows the findings of this survey.
From this pie chart answer the following:
(i) If 20 people liked classical music, how many young people were surveyed?
(ii) Which type of music is liked by the maximum number of people?
(iii) If a cassette company were to make 1000 CD’s, how many of each type would they make?
Answer:
From the given pie chart, the preferences for different types of music are as follows:
Classical: $10\%$
Semi Classical: $20\%$
Light: $40\%$
Folk: $30\%$
(i) If 20 people liked classical music, how many young people were surveyed?
We are given that the number of people who liked Classical music is 20.
From the pie chart, the percentage of people who liked Classical music is $10\%$.
Let the total number of young people surveyed be N.
So, $10\%$ of N is equal to 20.
$\frac{10}{100} \times N = 20$
$\frac{1}{10} \times N = 20$
To find N, multiply both sides by 10:
$N = 20 \times 10$
$N = 200$
Therefore, 200 young people were surveyed.
(ii) Which type of music is liked by the maximum number of people?
To find the type of music liked by the maximum number of people, we need to look for the music type with the highest percentage in the pie chart.
Comparing the percentages: Classical ($10\%$), Semi Classical ($20\%$), Light ($40\%$), Folk ($30\%$).
The highest percentage is $40\%$, which corresponds to Light music.
Therefore, Light music is liked by the maximum number of people.
(iii) If a cassette company were to make 1000 CD’s, how many of each type would they make?
The total number of CD's to be made is 1000.
The number of CD's for each type should be proportional to the percentage of people who liked that type of music from the survey.
Number of CD's for Classical music = $10\%$ of 1000
= $\frac{10}{100} \times 1000 = \frac{1}{10} \times 1000 = 100$
Number of CD's for Semi Classical music = $20\%$ of 1000
= $\frac{20}{100} \times 1000 = \frac{1}{5} \times 1000 = 200$
Number of CD's for Light music = $40\%$ of 1000
= $\frac{40}{100} \times 1000 = \frac{2}{5} \times 1000 = 400$
Number of CD's for Folk music = $30\%$ of 1000
= $\frac{30}{100} \times 1000 = \frac{3}{10} \times 1000 = 300$
So, the company would make:
100 CD's of Classical music.
200 CD's of Semi Classical music.
400 CD's of Light music.
300 CD's of Folk music.
Question 2. A group of 360 people were asked to vote for their favourite season from the three seasons rainy, winter and summer.
| Season | No. of Votes |
| Summer | 90 |
| Rainy | 120 |
| Winter | 150 |
(i) Which season got the most votes?
(ii) Find the central angle of each sector.
(iii) Draw a pie chart to show this information.
Answer:
Solution:
Given:
Number of people surveyed: 360
Votes for Summer: 90
Votes for Rainy: 120
Votes for Winter: 150
(i) Which season got the most votes?
We need to compare the number of votes received by each season.
Summer: 90 votes
Rainy: 120 votes
Winter: 150 votes
Comparing the numbers 90, 120, and 150, the highest number is 150.
The season that received 150 votes is Winter.
Therefore, the Winter season got the most votes.
(ii) Find the central angle of each sector.
The total number of votes represents the whole circle in the pie chart, which corresponds to a central angle of $360^\circ$. The total number of votes is 360.
The central angle for each season is a fraction of $360^\circ$, where the fraction is the number of votes for the season divided by the total number of votes.
Central Angle = $\frac{\text{Number of Votes}}{\text{Total Votes}} \times 360^\circ$
Let's calculate the central angle for each season:
Central angle for Summer = $\frac{90}{360} \times 360^\circ$
Central angle for Summer = $\frac{\cancel{90}^{1}}{\cancel{360}_{4}} \times 360^\circ = \frac{1}{4} \times 360^\circ = 90^\circ$
Central angle for Rainy = $\frac{120}{360} \times 360^\circ$
Central angle for Rainy = $\frac{\cancel{120}^{1}}{\cancel{360}_{3}} \times 360^\circ = \frac{1}{3} \times 360^\circ = 120^\circ$
Central angle for Winter = $\frac{150}{360} \times 360^\circ$
Central angle for Winter = $\frac{150}{\cancel{360}} \times \cancel{360}^\circ = 150^\circ$
We can verify the sum of the central angles: $90^\circ + 120^\circ + 150^\circ = 360^\circ$.
The central angles for each sector are: Summer: $90^\circ$, Rainy: $120^\circ$, Winter: $150^\circ$.
(iii) Draw a pie chart to show this information.
To draw the pie chart, follow these steps:
1. Draw a circle of any convenient radius using a compass.
2. Draw a radius from the centre of the circle. This will be the starting line for the first sector.
3. Using a protractor, draw the first sector with a central angle of $90^\circ$ (for Summer), starting from the radius drawn in step 2. Draw a line from the centre to the circumference to mark the end of this sector.
4. From the end line of the first sector, draw the second sector with a central angle of $120^\circ$ (for Rainy).
5. The remaining portion of the circle should represent the Winter season, and its central angle should be $150^\circ$. Check if the last line aligns with the original starting radius.
6. Label each sector clearly with the name of the season and optionally the number of votes or the percentage.
7. Give the pie chart a suitable title, such as "Favourite Seasons".
Question 3. Draw a pie chart showing the following information. The table shows the colours preferred by a group of people.
| Colours | Number of People |
| Blue | 18 |
| Green | 9 |
| Red | 6 |
| Yellow | 3 |
| Total | 36 |
Find the proportion of each sector. For example, Blue is $\frac{18}{36}$ = $\frac{1}{2}$ ; Green is $\frac{9}{36}$ = $\frac{1}{4}$ and so on. Use this to find the corresponding angles.
Answer:
Given:
The table shows the number of people who preferred different colours:
Blue: 18 people
Green: 9 people
Red: 6 people
Yellow: 3 people
Total number of people: $18 + 9 + 6 + 3 = 36$
To Draw:
A pie chart for the given data.
Solution:
To draw a pie chart, we need to find the central angle of the sector for each colour. The sum of the central angles in a pie chart is $360^\circ$. The central angle for each colour is a fraction of $360^\circ$, based on the proportion of people who preferred that colour out of the total number of people.
The central angle for each component is calculated as:
Central Angle for a colour = $\frac{\text{Number of people for the colour}}{\text{Total number of people}} \times 360^\circ$
Let's calculate the central angle for each colour:
For Blue:
Fraction = $\frac{18}{36} = \frac{1}{2}$
Central Angle = $\frac{1}{2} \times 360^\circ = 180^\circ$
For Green:
Fraction = $\frac{9}{36} = \frac{1}{4}$
Central Angle = $\frac{1}{4} \times 360^\circ = 90^\circ$
For Red:
Fraction = $\frac{6}{36} = \frac{1}{6}$
Central Angle = $\frac{1}{6} \times 360^\circ = 60^\circ$
For Yellow:
Fraction = $\frac{3}{36} = \frac{1}{12}$
Central Angle = $\frac{1}{12} \times 360^\circ = 30^\circ$
Let's verify the sum of the central angles: $180^\circ + 90^\circ + 60^\circ + 30^\circ = 360^\circ$. The sum is correct.
We can summarize the data with calculated central angles in a table:
| Colours | Number of People | Fraction of Total | Central Angle |
| Blue | 18 | $\frac{18}{36} = \frac{1}{2}$ | $\frac{1}{2} \times 360^\circ = 180^\circ$ |
| Green | 9 | $\frac{9}{36} = \frac{1}{4}$ | $\frac{1}{4} \times 360^\circ = 90^\circ$ |
| Red | 6 | $\frac{6}{36} = \frac{1}{6}$ | $\frac{1}{6} \times 360^\circ = 60^\circ$ |
| Yellow | 3 | $\frac{3}{36} = \frac{1}{12}$ | $\frac{1}{12} \times 360^\circ = 30^\circ$ |
| Total | 36 | $\frac{36}{36} = 1$ | $180^\circ + 90^\circ + 60^\circ + 30^\circ = 360^\circ$ |
Now, we can draw the pie chart using these central angles.
Steps to draw the pie chart:
1. Draw a circle with any convenient radius using a compass.
2. Draw a radius from the centre of the circle. This will be the starting line for the first sector.
3. Using a protractor, draw the first sector with a central angle of $180^\circ$ (for Blue), starting from the initial radius. Draw a line from the centre to the circumference to mark the end of this sector.
4. From the end line of the first sector, draw the second sector with a central angle of $90^\circ$ (for Green).
5. From the end line of the second sector, draw the third sector with a central angle of $60^\circ$ (for Red).
6. The remaining portion of the circle should represent the Yellow colour, and its central angle should be $30^\circ$. Check if the last line aligns with the original starting radius.
7. Label each sector clearly with the name of the colour and optionally the number of people or the percentage.
8. Give the pie chart a suitable title, such as "Colour Preference".
Question 4. The adjoining pie chart gives the marks scored in an examination by a student in Hindi, English, Mathematics, Social Science and Science. If the total marks obtained by the students were 540, answer the following questions.
(i) In which subject did the student score 105 marks?
(Hint: for 540 marks, the central angle = 360°. So, for 105 marks, what is the central angle?)
(ii) How many more marks were obtained by the student in Mathematics than in Hindi?
(iii) Examine whether the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi.
(Hint: Just study the central angles).

Answer:
Given:
Total marks obtained by the student = 540.
The adjoining pie chart shows the distribution of marks in different subjects using central angles:
Hindi: $70^\circ$
English: $55^\circ$
Mathematics: $90^\circ$
Social Science: $65^\circ$
Science: $80^\circ$
To Find:
(i) The subject in which the student scored 105 marks.
(ii) How many more marks were obtained by the student in Mathematics than in Hindi.
(iii) Whether the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi.
Solution:
The total central angle of a pie chart represents the total quantity. Here, the total angle $360^\circ$ represents the total marks, which is 540.
We can establish a relationship between the central angle and the marks obtained.
Value of $1^\circ$ central angle in terms of marks = $\frac{\text{Total Marks}}{\text{Total Angle}} = \frac{540}{360} = \frac{54}{36} = \frac{3}{2} = 1.5$ marks.
Value of 1 mark in terms of central angle = $\frac{\text{Total Angle}}{\text{Total Marks}} = \frac{360}{540} = \frac{36}{54} = \frac{2}{3}$ degrees.
(i) In which subject did the student score 105 marks?
We need to find the central angle that corresponds to 105 marks.
Central angle for 105 marks = $105 \times \frac{2}{3}$ degrees
= $\frac{105 \times 2}{3}^\circ = 35 \times 2^\circ = 70^\circ$
The central angle corresponding to 105 marks is $70^\circ$.
Looking at the pie chart, the subject with a central angle of $70^\circ$ is Hindi.
Therefore, the student scored 105 marks in Hindi.
(ii) How many more marks were obtained by the student in Mathematics than in Hindi?
First, we calculate the marks obtained in Mathematics and Hindi.
Marks in Mathematics = Central angle for Mathematics $\times$ Value of $1^\circ$ in marks
= $90^\circ \times 1.5 = 90 \times \frac{3}{2} = 45 \times 3 = 135$ marks.
Marks in Hindi = Central angle for Hindi $\times$ Value of $1^\circ$ in marks
= $70^\circ \times 1.5 = 70 \times \frac{3}{2} = 35 \times 3 = 105$ marks.
The difference in marks between Mathematics and Hindi is:
Difference = Marks in Mathematics - Marks in Hindi
= $135 - 105 = 30$ marks.
The student obtained 30 more marks in Mathematics than in Hindi.
(iii) Examine whether the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi.
As suggested by the hint, we can compare the sum of marks by comparing the sum of their corresponding central angles. Since the marks are directly proportional to the central angles, a larger sum of angles implies a larger sum of marks.
Sum of central angles for Social Science and Mathematics = Central angle (Social Science) + Central angle (Mathematics)
= $65^\circ + 90^\circ = 155^\circ$
Sum of central angles for Science and Hindi = Central angle (Science) + Central angle (Hindi)
= $80^\circ + 70^\circ = 150^\circ$
Comparing the sums of the central angles:
$155^\circ > 150^\circ$
Since the sum of the central angles for Social Science and Mathematics ($155^\circ$) is greater than the sum of the central angles for Science and Hindi ($150^\circ$), the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi.
Therefore, the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi.
Alternative approach for part (iii) (by calculating marks):
Marks in Social Science = $65^\circ \times 1.5 = 65 \times \frac{3}{2} = \frac{195}{2} = 97.5$ marks.
Marks in Mathematics = 135 marks (calculated in part ii).
Sum (Social Science + Mathematics) = $97.5 + 135 = 232.5$ marks.
Marks in Science = $80^\circ \times 1.5 = 80 \times \frac{3}{2} = 40 \times 3 = 120$ marks.
Marks in Hindi = 105 marks (calculated in part ii).
Sum (Science + Hindi) = $120 + 105 = 225$ marks.
Comparing the sums of marks: $232.5$ vs $225$.
Since $232.5 > 225$, the sum of marks obtained in Social Science and Mathematics is more than that in Science and Hindi.
Question 5. The number of students in a hostel, speaking different languages is given below. Display the data in a pie chart.
| Language | Hindi | English | Marathi | Tamil | Bengali | Total |
|---|---|---|---|---|---|---|
| Number of Students | 40 | 12 | 9 | 7 | 4 | 72 |
Answer:
Given:
The table shows the number of students in a hostel speaking different languages.
Hindi: 40 students
English: 12 students
Marathi: 9 students
Tamil: 7 students
Bengali: 4 students
Total number of students: $40 + 12 + 9 + 7 + 4 = 72$
To Display:
The data in a pie chart.
Solution:
To display the data in a pie chart, we need to find the central angle of the sector for each language. The total number of students (72) represents the whole circle in the pie chart, which corresponds to a central angle of $360^\circ$.
The central angle for each language is a fraction of $360^\circ$, where the fraction is the number of students speaking that language divided by the total number of students.
Central Angle = $\frac{\text{Number of Students for the Language}}{\text{Total Number of Students}} \times 360^\circ$
Let's calculate the central angle for each language:
Hindi:
Fraction = $\frac{40}{72}$
Central Angle = $\frac{\cancel{40}^{5}}{\cancel{72}_{9}} \times \cancel{360}^\circ = \frac{5}{9} \times 360^\circ = 5 \times 40^\circ = 200^\circ$
English:
Fraction = $\frac{12}{72} = \frac{1}{6}$
Central Angle = $\frac{1}{6} \times 360^\circ = 60^\circ$
Marathi:
Fraction = $\frac{9}{72} = \frac{1}{8}$
Central Angle = $\frac{1}{8} \times 360^\circ = 45^\circ$
Tamil:
Fraction = $\frac{7}{72}$
Central Angle = $\frac{7}{72} \times 360^\circ = 7 \times 5^\circ = 35^\circ$
Bengali:
Fraction = $\frac{4}{72} = \frac{1}{18}$
Central Angle = $\frac{1}{18} \times 360^\circ = 20^\circ$
Let's verify the sum of the central angles: $200^\circ + 60^\circ + 45^\circ + 35^\circ + 20^\circ = 360^\circ$. The sum is correct.
We can summarize the data with calculated central angles in a table:
| Language | Number of Students | Fraction of Total Students | Central Angle |
| Hindi | 40 | $\frac{40}{72}$ | $200^\circ$ |
| English | 12 | $\frac{12}{72} = \frac{1}{6}$ | $60^\circ$ |
| Marathi | 9 | $\frac{9}{72} = \frac{1}{8}$ | $45^\circ$ |
| Tamil | 7 | $\frac{7}{72}$ | $35^\circ$ |
| Bengali | 4 | $\frac{4}{72} = \frac{1}{18}$ | $20^\circ$ |
| Total | 72 | $\frac{72}{72} = 1$ | $360^\circ$ |
Now, we can draw the pie chart using these central angles.
Steps to draw the pie chart:
1. Draw a circle with any convenient radius using a compass.
2. Draw a radius from the centre of the circle. This will be the starting line for the first sector.
3. Using a protractor, draw the sectors with the calculated central angles ($200^\circ$, $60^\circ$, $45^\circ$, $35^\circ$, $20^\circ$) sequentially from the end of the previous sector. Draw lines from the centre to the circumference to mark the boundaries of each sector.
4. Label each sector clearly with the name of the language and optionally the number of students or the percentage.
5. Give the pie chart a suitable title, such as "Languages Spoken by Students in a Hostel".
Example 3 (Before Exercise 4.2)
Example 3: A bag has 4 red balls and 2 yellow balls. (The balls are identical in all respects other than colour). A ball is drawn from the bag without looking into the bag. What is probability of getting a red ball? Is it more or less than getting a yellow ball?
Answer:
Given:
Number of red balls = 4
Number of yellow balls = 2
Total number of balls in the bag = Number of red balls + Number of yellow balls = $4 + 2 = 6$
To Find:
1. The probability of getting a red ball.
2. Whether the probability of getting a red ball is more or less than getting a yellow ball.
Solution:
The probability of an event is defined as the ratio of the number of favourable outcomes to the total number of possible outcomes.
$P(\text{Event}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
1. Probability of getting a red ball:
Number of favourable outcomes (getting a red ball) = 4
Total number of possible outcomes (total balls in the bag) = 6
Probability of getting a red ball, $P(\text{Red}) = \frac{4}{6}$
We simplify the fraction:
$P(\text{Red}) = \frac{\cancel{4}^{2}}{\cancel{6}_{3}} = \frac{2}{3}$
2. Comparison of probabilities:
First, we find the probability of getting a yellow ball.
Number of favourable outcomes (getting a yellow ball) = 2
Total number of possible outcomes (total balls in the bag) = 6
Probability of getting a yellow ball, $P(\text{Yellow}) = \frac{2}{6}$
We simplify the fraction:
$P(\text{Yellow}) = \frac{\cancel{2}^{1}}{\cancel{6}_{3}} = \frac{1}{3}$
Now, we compare $P(\text{Red})$ and $P(\text{Yellow})$.
$P(\text{Red}) = \frac{2}{3}$
$P(\text{Yellow}) = \frac{1}{3}$
To compare fractions with the same denominator, we compare their numerators. Here, the denominator is 3.
Comparing the numerators: 2 and 1.
Since $2 > 1$, it means $\frac{2}{3} > \frac{1}{3}$.
Therefore, $P(\text{Red}) > P(\text{Yellow})$.
Conclusion:
The probability of getting a red ball is $\frac{2}{3}$ and the probability of getting a yellow ball is $\frac{1}{3}$.
Since the probability of getting a red ball ($\frac{2}{3}$) is greater than the probability of getting a yellow ball ($\frac{1}{3}$), the probability of getting a red ball is more than the probability of getting a yellow ball.
Exercise 4.2
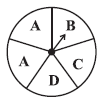
Question 1. List the outcomes you can see in these experiments.
(a) Spinning a wheel
(b) Tossing two coins together
Answer:
Here are the possible outcomes for each experiment:
(a) Spinning a wheel
Looking at the provided figure, the wheel is divided into sectors labeled A, B, C, D, and A again. When the wheel is spun, the pointer can land on any of these sectors.
The possible outcomes are the labels of the sectors.
The outcomes are: A, B, C, D, A.
If we consider the distinct outcomes (i.e., ignoring repetitions), the outcomes are: A, B, C, D.
(b) Tossing two coins together
When a single coin is tossed, there are two possible outcomes: Head (H) or Tail (T).
When two coins are tossed together, the outcome is a pair of results from each coin. Let's list the possibilities:
Coin 1 is Head and Coin 2 is Head (HH)
Coin 1 is Head and Coin 2 is Tail (HT)
Coin 1 is Tail and Coin 2 is Head (TH)
Coin 1 is Tail and Coin 2 is Tail (TT)
The possible outcomes when tossing two coins together are: HH, HT, TH, TT.
Question 2. When a die is thrown, list the outcomes of an event of getting
(i) (a) a prime number (b) not a prime number.
(ii) (a) a number greater than 5 (b) a number not greater than 5.
Answer:
When a die is thrown, the possible outcomes are the numbers on its faces: 1, 2, 3, 4, 5, 6.
The sample space of outcomes is {1, 2, 3, 4, 5, 6}.
(i) (a) getting a prime number
Prime numbers in the sample space are numbers greater than 1 that are only divisible by 1 and themselves.
The prime numbers in {1, 2, 3, 4, 5, 6} are 2, 3, and 5.
The outcomes of the event "getting a prime number" are: {2, 3, 5}.
(i) (b) not a prime number
These are the outcomes in the sample space that are not prime numbers.
The numbers in {1, 2, 3, 4, 5, 6} that are not prime are 1, 4, and 6.
The outcomes of the event "getting not a prime number" are: {1, 4, 6}.
(ii) (a) a number greater than 5
We need to find the numbers in the sample space {1, 2, 3, 4, 5, 6} that are greater than 5.
Only the number 6 is greater than 5.
The outcomes of the event "getting a number greater than 5" are: {6}.
(ii) (b) a number not greater than 5
These are the numbers in the sample space {1, 2, 3, 4, 5, 6} that are less than or equal to 5.
The numbers not greater than 5 are 1, 2, 3, 4, and 5.
The outcomes of the event "getting a number not greater than 5" are: {1, 2, 3, 4, 5}.
Question 3. Find the.
(a) Probability of the pointer stopping on D in (Question 1-(a))?
(b) Probability of getting an ace from a well shuffled deck of 52 playing cards?
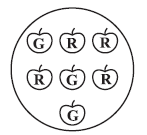
(c) Probability of getting a red apple. (See figure below)
Answer:
We need to find the probability for three different events.
Recall the formula for probability:
$P(\text{Event}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(a) Probability of the pointer stopping on D in (Question 1-(a))?
From Question 1(a), the spinning wheel has sectors labelled A, B, C, D, A.
Total number of possible outcomes (the total number of sectors) = 5
Number of favourable outcomes (the number of sectors labelled D) = 1 (There is only one sector with D)
Probability of the pointer stopping on D is:
$P(\text{Stopping on D}) = \frac{\text{Number of D sectors}}{\text{Total number of sectors}} = \frac{1}{5}$
So, the probability of the pointer stopping on D is $\frac{1}{5}$.
(b) Probability of getting an ace from a well shuffled deck of 52 playing cards?
A standard deck of playing cards has 52 cards in total.
Total number of possible outcomes (the total number of cards) = 52
The event is getting an ace. There are 4 aces in a deck of 52 cards (Ace of Hearts, Ace of Diamonds, Ace of Clubs, Ace of Spades).
Number of favourable outcomes (the number of aces) = 4
Probability of getting an ace is:
$P(\text{Getting an ace}) = \frac{\text{Number of aces}}{\text{Total number of cards}} = \frac{4}{52}$
We simplify the fraction:
$P(\text{Getting an ace}) = \frac{\cancel{4}^{1}}{\cancel{52}_{13}} = \frac{1}{13}$
So, the probability of getting an ace is $\frac{1}{13}$.
(c) Probability of getting a red apple. (See figure below)
From the figure provided:
Let's count the total number of apples.
Total number of apples = 7 (4 red apples + 3 green apples)
Total number of possible outcomes (total number of apples) = 7
The event is getting a red apple.
Number of favourable outcomes (the number of red apples) = 4
Probability of getting a red apple is:
$P(\text{Getting a red apple}) = \frac{\text{Number of red apples}}{\text{Total number of apples}} = \frac{4}{7}$
So, the probability of getting a red apple is $\frac{4}{7}$.
Question 4. Numbers 1 to 10 are written on ten separate slips (one number on one slip), kept in a box and mixed well. One slip is chosen from the box without looking into it. What is the probability of .
(i) getting a number 6?
(ii) getting a number less than 6?
(iii) getting a number greater than 6?
(iv) getting a 1-digit number?
Answer:
The numbers on the ten separate slips are 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10.
The total number of possible outcomes when one slip is chosen is 10.
Total number of possible outcomes = 10.
The probability of an event is given by:
$P(\text{Event}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) getting a number 6?
The event is getting the number 6.
The number of favourable outcomes (slips with the number 6) is 1.
Probability of getting a number 6 = $P(6) = \frac{\text{Number of slips with 6}}{\text{Total number of slips}}$
$P(6) = \frac{1}{10}$
(ii) getting a number less than 6?
The event is getting a number less than 6.
The numbers less than 6 in the set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} are {1, 2, 3, 4, 5}.
The number of favourable outcomes is 5.
Probability of getting a number less than 6 = $P(\text{number} < 6) = \frac{\text{Number of slips with a number < 6}}{\text{Total number of slips}}$
$P(\text{number} < 6) = \frac{5}{10}$
Simplify the fraction:
$P(\text{number} < 6) = \frac{\cancel{5}^{1}}{\cancel{10}_{2}} = \frac{1}{2}$
(iii) getting a number greater than 6?
The event is getting a number greater than 6.
The numbers greater than 6 in the set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} are {7, 8, 9, 10}.
The number of favourable outcomes is 4.
Probability of getting a number greater than 6 = $P(\text{number} > 6) = \frac{\text{Number of slips with a number > 6}}{\text{Total number of slips}}$
$P(\text{number} > 6) = \frac{4}{10}$
Simplify the fraction:
$P(\text{number} > 6) = \frac{\cancel{4}^{2}}{\cancel{10}_{5}} = \frac{2}{5}$
(iv) getting a 1-digit number?
The event is getting a 1-digit number.
The 1-digit numbers in the set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} are {1, 2, 3, 4, 5, 6, 7, 8, 9}.
The number of favourable outcomes is 9.
Probability of getting a 1-digit number = $P(\text{1-digit number}) = \frac{\text{Number of slips with a 1-digit number}}{\text{Total number of slips}}$
$P(\text{1-digit number}) = \frac{9}{10}$
Question 5. If you have a spinning wheel with 3 green sectors, 1 blue sector and 1 red sector, what is the probability of getting a green sector? What is the probability of getting a non blue sector?
Answer:
Given:
Number of green sectors = 3
Number of blue sector = 1
Number of red sector = 1
The total number of sectors on the spinning wheel is the sum of sectors of all colours.
Total number of sectors = $3 + 1 + 1 = 5$
Total number of possible outcomes = 5.
To Find:
1. The probability of getting a green sector.
2. The probability of getting a non-blue sector.
Solution:
The probability of any event is given by the formula:
$P(\text{Event}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
1. Probability of getting a green sector:
The event is getting a green sector.
The number of favourable outcomes (getting a green sector) = 3 (since there are 3 green sectors).
The total number of possible outcomes (total sectors) = 5.
Probability of getting a green sector is:
$P(\text{Green}) = \frac{\text{Number of green sectors}}{\text{Total number of sectors}} = \frac{3}{5}$
2. Probability of getting a non-blue sector:
The event is getting a non-blue sector.
A non-blue sector means the sector is not blue. The sectors that are not blue are green and red.
Number of non-blue sectors = Number of green sectors + Number of red sectors = $3 + 1 = 4$
The number of favourable outcomes (getting a non-blue sector) = 4.
The total number of possible outcomes (total sectors) = 5.
Probability of getting a non-blue sector is:
$P(\text{Non-blue}) = \frac{\text{Number of non-blue sectors}}{\text{Total number of sectors}} = \frac{4}{5}$
Alternate method for Probability of getting a non-blue sector:
First, find the probability of getting a blue sector.
Number of favourable outcomes (getting a blue sector) = 1 (since there is 1 blue sector).
Total number of possible outcomes = 5.
Probability of getting a blue sector is:
$P(\text{Blue}) = \frac{\text{Number of blue sectors}}{\text{Total number of sectors}} = \frac{1}{5}$
The probability of not getting a blue sector (non-blue sector) is 1 minus the probability of getting a blue sector.
$P(\text{Non-blue}) = 1 - P(\text{Blue}) = 1 - \frac{1}{5} = \frac{5}{5} - \frac{1}{5} = \frac{4}{5}$
Conclusion:
The probability of getting a green sector is $\frac{3}{5}$.
The probability of getting a non-blue sector is $\frac{4}{5}$.
Question 6. Find the probabilities of the events given in Question 2.
Answer:
When a die is thrown, the total number of possible outcomes is 6. The sample space is {1, 2, 3, 4, 5, 6}.
The probability of an event is given by the formula:
$P(\text{Event}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) (a) getting a prime number
The prime numbers in the sample space {1, 2, 3, 4, 5, 6} are 2, 3, and 5.
Number of favourable outcomes = 3.
Total number of possible outcomes = 6.
Probability of getting a prime number = $P(\text{prime number}) = \frac{3}{6}$
Simplify the fraction:
$P(\text{prime number}) = \frac{\cancel{3}^{1}}{\cancel{6}_{2}} = \frac{1}{2}$
(i) (b) not a prime number
The numbers that are not prime in the sample space {1, 2, 3, 4, 5, 6} are 1, 4, and 6.
Number of favourable outcomes = 3.
Total number of possible outcomes = 6.
Probability of not getting a prime number = $P(\text{not prime number}) = \frac{3}{6}$
Simplify the fraction:
$P(\text{not prime number}) = \frac{\cancel{3}^{1}}{\cancel{6}_{2}} = \frac{1}{2}$
(ii) (a) a number greater than 5
The number greater than 5 in the sample space {1, 2, 3, 4, 5, 6} is 6.
Number of favourable outcomes = 1.
Total number of possible outcomes = 6.
Probability of getting a number greater than 5 = $P(\text{number} > 5) = \frac{1}{6}$
(ii) (b) a number not greater than 5
The numbers not greater than 5 in the sample space {1, 2, 3, 4, 5, 6} are 1, 2, 3, 4, and 5.
Number of favourable outcomes = 5.
Total number of possible outcomes = 6.
Probability of getting a number not greater than 5 = $P(\text{number} \leq 5) = \frac{5}{6}$

